Ali Kaya
“There was a footpath leading across the fields to New Southgate, and I used to go there alone to watch the sunset and contemplate suicide. I did not, however, commit suicide, because I wished to know more about mathematics.”
-Bertrand Russell, Nobel Laureate and Mathematician
It is mystical when you step outside on a snowy morning. Snowflakes are swirling around the vast sky and falling and blanketing the ground. If a snowflake lands on you, it is like a winter angel. There are no flowers around, for they cannot survive the cold; yet what lies before your eyes is an incredible beauty. And it’s remarkable, you come to realize, that no two snowflakes are alike. It is as if the uniqueness of a snowflake is controlled by a divine force. The individuality of a snowflake’s structure draws a parallel to human life. Like snowflakes, everyone has a unique story to tell.
I am not the only one who ponders about snowflakes; many mathematicians do the same. Actually, they think about the characteristics of snowflakes because they are particularly important for three basic mathematical principles: pattern, symmetry, and symmetry breaking.
A little-known scientist, Wilson Bentley, a.k.a. “the Snowflake Man” took pictures of snowflakes almost every day and observed them until he died. You can buy his book about his work on Amazon. If you wish to know why he did it, read about it at snowflakebentley.com.![]()
“Under the microscope, I found that snowflakes were miracles of nature; and it seemed a shame that this beauty should not be seen and appreciated by others. Every crystal was a masterpiece of design and no one design was ever repeated. When a snowflake melted, that design was forever lost. That beauty was gone, without leaving any record behind.”
-Wilson Bentley
When I checked the Oxford dictionary, there were 3 definitions for the word “pattern.” Two of these definitions [listed below] are important for this article.
Pattern: 1. A repeated decorative design; 2. An example for others to follow.
When we check the pictures and delve deeper into each snowflake, we will see that the structures of the snowflakes are totally different. However, they have something in common: symmetry and a hexagonal structure.
These perfect ice crystals are genuine, even though it is hard to believe they are not fake.
When I take a close look at a snowflake, the beauty of the combination of ice molecules fascinates me every time; each flake is unique. However, uniqueness is not the point here. The things that make snowflakes important objects for mathematicians are their symmetry and their hexagonal structure. Math-loving people have a lot of interest in transformations. They love moving objects. And, surprisingly, if an object is symmetric, transformations are not even noticed by many.
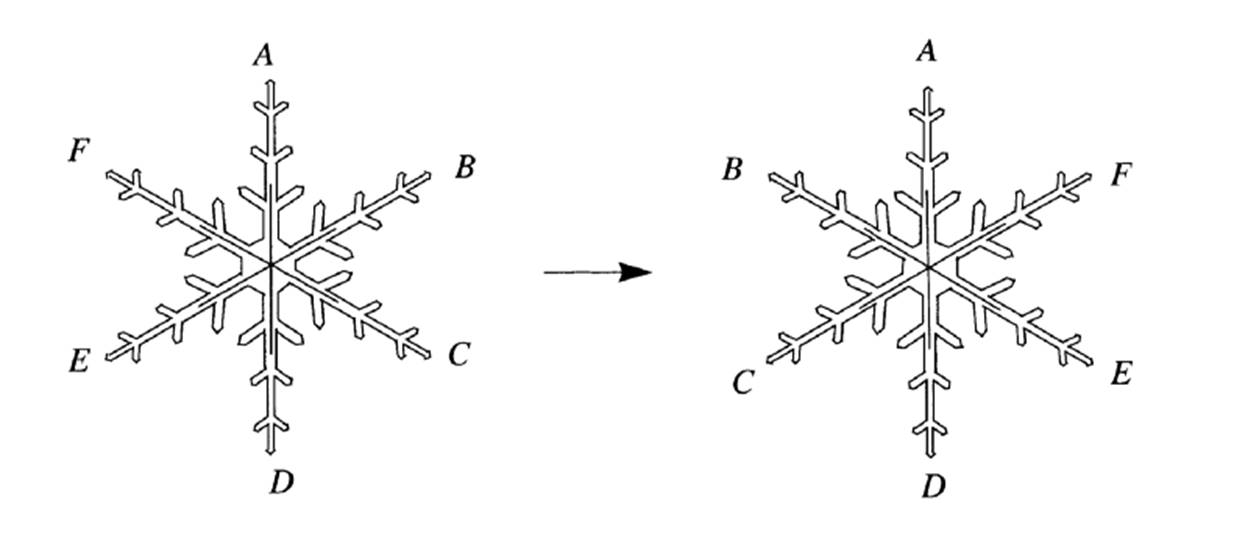
To be more precise, when you have a hexagonal symmetric snowflake, or any other symmetrical object, when you rotate it in any direction, 60°, 120°, 180°, 240°, 300°, or 360°, people watching you wouldn’t realize it. If you check the images below, you will see rotated shapes but no difference. It appears to be the same shape in exactly the same place. 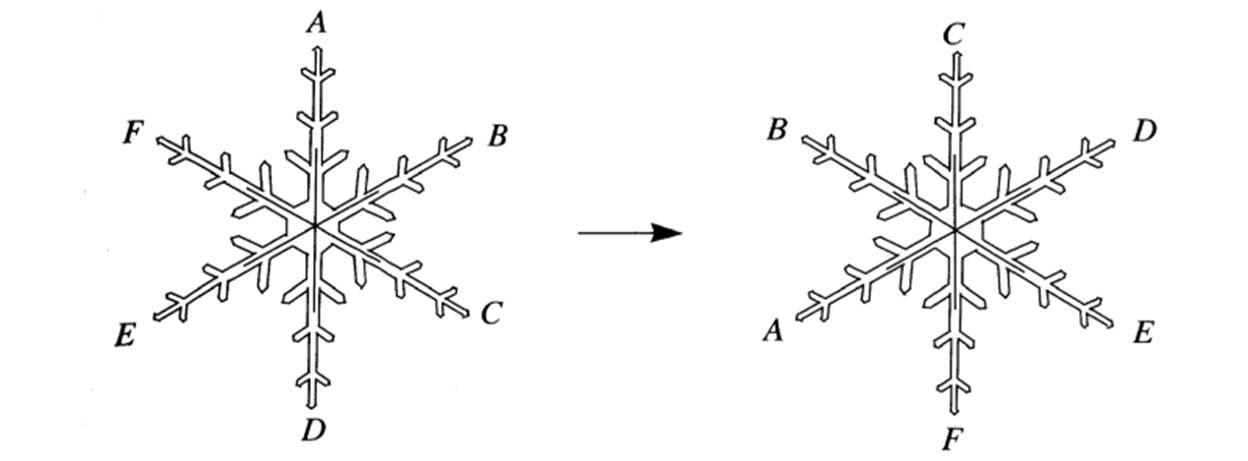
1- Counterclockwise rotation by 120°
2- Reflection through a vertical axis
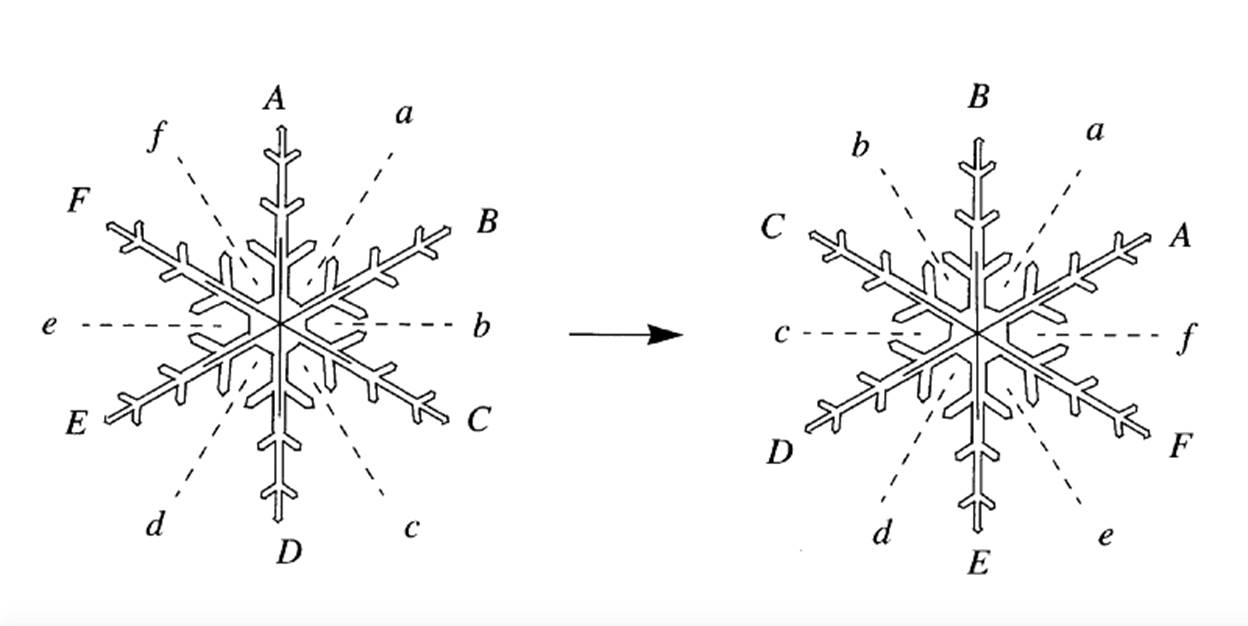
3- Reflection axes of a snowflake[1]
Snowflakes also possess reflectional symmetry. If we stand in front of a mirror, our reflection looks exactly the same. Hence, if we put a mirror in the middle of a snowflake, there will be a reflection. For a snowflake, we can put a mirror 6 different ways. Thus, we can say that a snowflake has 12 symmetries: 6 from reflections, and 6 from rotations.[2]
Now we can define symmetry as a transformation that leaves things unchanged. We can also claim that a combination of any of the transformations will give us exactly the same shape. For instance, we can rotate our snowflake 60° two or three times in a row and flip it over, and it will remain unchanged.
At this point, you might ask the question: “You have all these fancy symmetries for this particular snowflake. But, does every snowflake possess the same symmetries?”
Snow is a molecular structure of an ice crystal. And ice is a structured substance. It is a different form of water. When the water cools down, the molecules move more slowly, and this begins to impact how the molecules line up. Hydrogen atoms of one water molecule bond with two oxygen atoms. As the water freezes, the molecules arrange into hexagonal patterns. They prefer to stay as far away from each other as possible, and that makes them take up more space. The large space affects density. The density of ice becomes less dense than water. This is why ice floats. Almost all other liquids have a higher density when they freeze.
When we examine an ice crystal carefully under normal conditions, we always see a combination of molecules with six-fold symmetry. Snowflake molecules make a honeycomb structure. This results in an inordinate amount of hexagonal symmetry in these molecular three-dimensional structures.
Okay, we saw the structure of a snowflake under normal conditions. But, what if we changed those conditions? Johannes Kepler answered this question after his experiments and wrote a book about snowflakes, particularly The Six-Cornered Snowflake.
There are two key elements which affect the structure of a snowflake: temperature and moisture. Each time the temperature or the amount of moisture change, the structure of a snowflake changes. If you check the snow crystal morphology diagram below, you will see that when the temperature nears 0° and humidity is high, the structure of a snowflake will be flowery. Flowery structures are called dendrites. When you make it a little bit colder, the structure will be fancy hexagonal plates. We can apply many combinations and get varying structures.
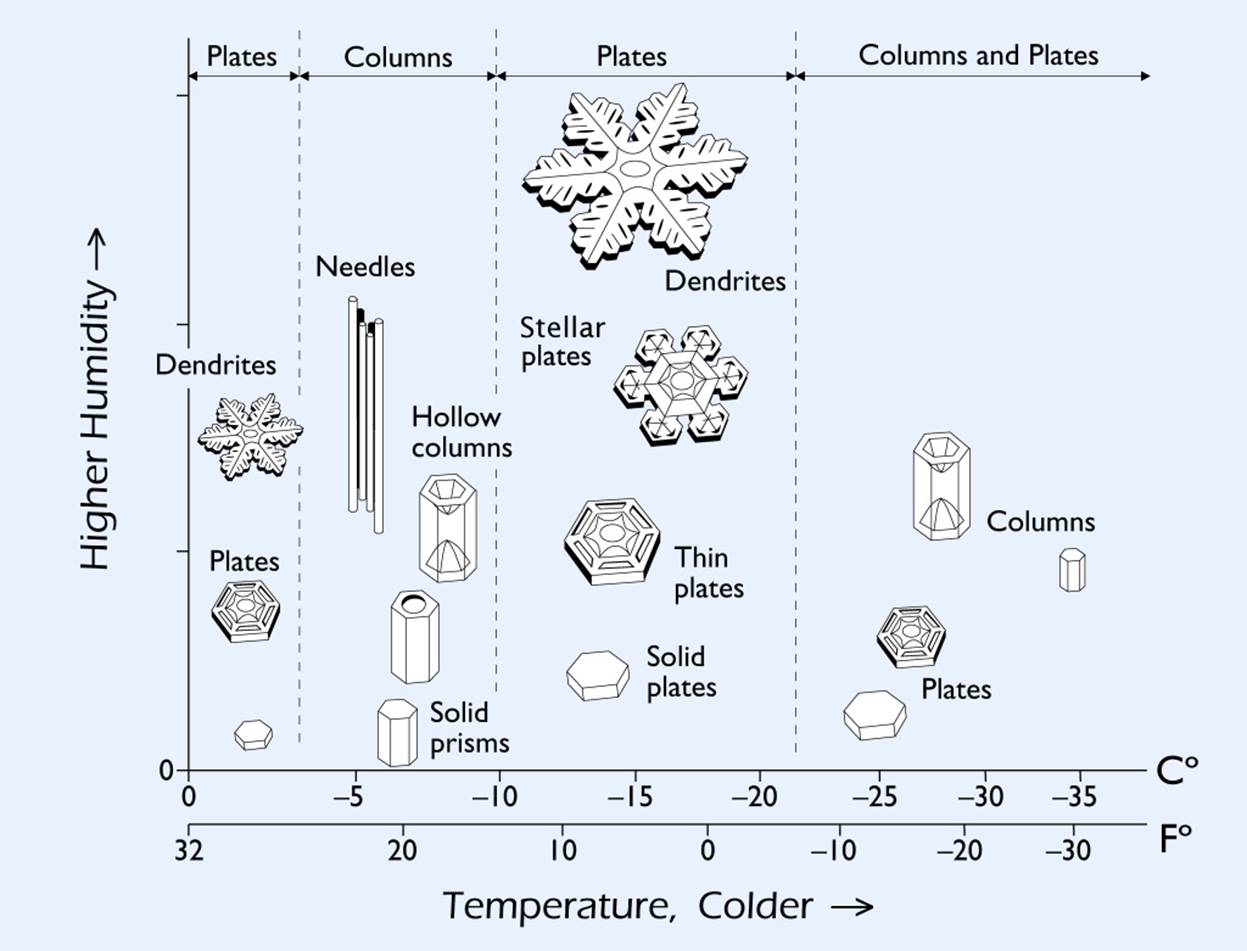
The Snow Crystal Morphology Diagram. Source: Snow Crystals - http://www.snowcrystals.com/science/science.html
Professor of physics Kenneth G. Libbrecht is the owner of the diagram below. In a PBS interview, he said, “It’s a mystery as to why snowflake shapes go from plates to columns to plates to columns as the temperature lowers. That’s one of the things I’ve been trying to understand. It has been a mystery for about 75 years, and it’s still unsolved.”[3]
The Shapes of Snowflakes | Source
In the end, although the structure of (almost) all snowflakes are the same, some of them are not completely hexagonal. For instance, there are some snowflakes that have tree structures. Some snowflakes have branches, and each branch has tiny branches.
But, why is the structure of some snowflakes not hexagonal?
So far, we have talked about pictures which were taken at a particular instant. We have seen the pictures of the motion of the snowflakes for the smallest amount of time that can be measured. However, a snowflake never stops spinning in the air. They tend to oscillate. That means the shape of the snowflake is changing all the time. But how? When you see a snowflake in the air, it changes its place after a second because it would be whirled about, and it will be under different conditions at that time. This process will occur up until the snowflake lands on the ground. We know from the diagram that the temperature and amount of moisture always affect the shape of a snowflake. While small-scale conditions are almost the same, on a larger-time scale, conditions will differ. And these differences will change every corner of a hexagonal snowflake, resulting in a different structure. This is the main reason behind the variety of snowflake structures and uniqueness.
In conclusion, we can say that a snowflake can preserve its six-fold symmetry at all times. I think we have another reason to love mathematics! I want to finish my piece with Hermann Hankel’s words:
“In most sciences one generation tears down what another has built, and what one has established another undoes. In mathematics alone, each generation adds a new story to the old structure.”